- 3.1 神经网络概述(Neural Network Overview)
- 3.2 神经网络的表示（Neural Network representation）
- 2.3 逻辑回归的代价函数(Logistic Regression Cost Function)
- 2.4 梯度下降法(Gradient Descent)
3.1 神经网络概述(Neural Network Overview)
神经网络看起来是如下这个样子，把许多sigmoid单元堆叠起来形成一个神经网络
3.2 神经网络的表示（Neural Network representation）
本节主要介绍逻辑回归的Hypothesis Function(假设函数)
2.3 逻辑回归的代价函数(Logistic Regression Cost Function)
为什么需要代价函数
为了训练逻辑回归模型的参数$w$和$b$，我们需要一个代价函数，通过训练代价函数得到参数$w$和$b$，逻辑回归的输出函数
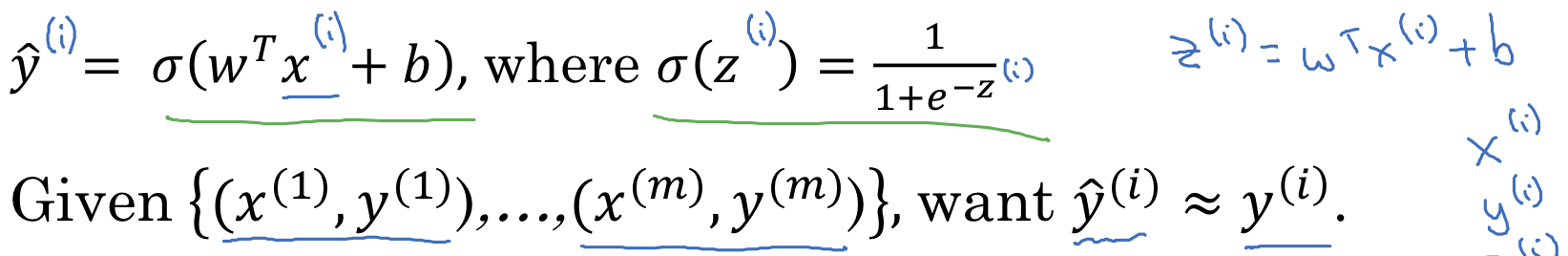为了让模型学习调整参数，需要给予一个$m$样本的训练集，在训练集上找到参数$w$和$b$,来得到输出，我们希望训练集的预测值$\hat{y}$接近于实际值$y$, 上标$(i)$表示第$i$个样本
损失函数（Loss Function)：
损失函数用来衡量预测值和实际值有多接近，损失函数是在单个样本中定义的，它衡量的是算法在单个样本中的表现。
逻辑回归中用到的损失函数是：$L\left( \hat{y},y \right)=-y\log(\hat{y})-(1-y)\log (1-\hat{y})$
代价函数(Cost Function)
算法的代价函数衡量算法在全体训练样本上的表现，是对$m$个样本的损失函数求和然后除以$m$:
2.4 梯度下降法(Gradient Descent)
逻辑回归的代价函数（成本函数）$J(w,b)$是含有两个参数的, $\partial$表示求偏导符号，可以读作round，$\frac{\partial J(w,b)}{\partial w}$就是函数$J(w,b)$对$w$求偏导, 在代码中我们会使用$dw$ 表示这个结果， $\frac{\partial J(w,b)}{\partial b}$ 就是函数$J(w,b)$对$b$ 求偏导，在代码中我们会使用$db$ 表示这个结果， 小写字母$d$ 用在求导数（derivative），即函数只有一个参数， 偏导数符号$\partial $ 用在求偏导（partial derivative），即函数含有两个以上的参数
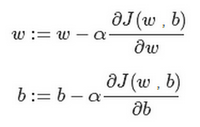迭代就是不断重复做如图的公式:
$:=$表示更新参数,
$a $ 表示学习率（learning rate），用来控制步长（step），即向下走一步的长度$\frac{dJ(w)}{dw}$ 就是函数$J(w)$对$w$ 求导（derivative），在代码